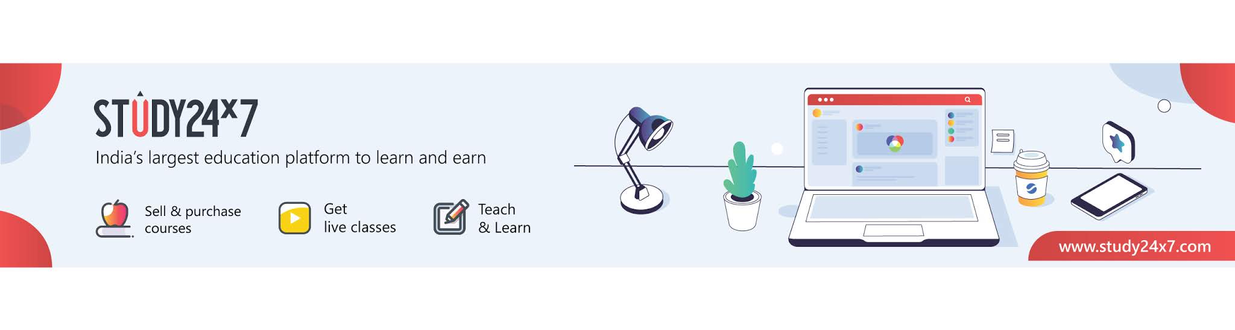
+91


(+93) Afghanistan

(+355) Albania

(+973) Bahrain

(+880) Bangladesh

(+32) Belgium

(+855) Cambodia

(+45) Denmark

(+20) Egypt

(+358) Finland

(+33) France

(+995) Georgia

(+49) Germany

(+233) Ghana

(+224) Guinea

(+348) Hungary

(+91) India

(+960) Maldives

(+230) Mauritius

(+52) Mexico

(+977) Nepal

(+31) Netherlands

(+64) New Zealand

(+234) Nigeria

(+968) Oman

(+92) Pakistan

(+48) Poland

(+351) Portugal

(+7) Russia
(+966) Saudi Arabia

(+27) South Africa

(+82) South Korea

(+34) Spain

(+268) Swaziland

(+46) Sweden

(+41) Switzerland

(+992) Tajikistan

(+90) Turkey

(+380) Ukraine

(+971) United Arab Emirates

(+44) United Kingdom

(+1) United States

(+263) Zimbabwe
Resend OTP
countDisplay
Cancel

























 999
999



















 5.0
5.0